Calculating the area of regular shapes is straightforward, but irregular figures can be trickier. However, with a few tools and techniques, you can estimate the area of an irregular figure accurately.
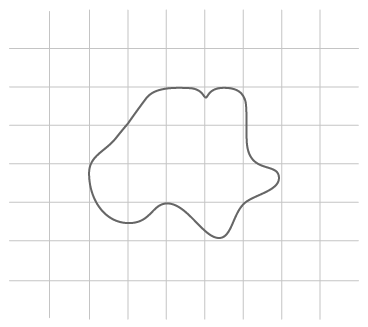
Step-by-Step Guide to Calculating the Area of an Irregular Figure
- Trace the Figure onto Transparent Paper: Begin by creating a copy of the irregular shape on a transparent sheet. This tracing will make it easier to overlay the figure on grid paper.
- Overlay on Grid Paper: Place the traced figure onto a piece of grid (or graph) paper. Make sure the grid squares are clear and easy to count. This grid will allow you to estimate the area by counting the squares.
- Count the Full Squares Inside the Shape: Begin by counting the number of squares that are entirely enclosed within the shape. Each full square represents one unit of area. Keep a tally of these complete squares as they provide the bulk of the area calculation.
- Count Squares More than Half Inside: Next, count the squares that are mostly enclosed by the shape (those that have more than half of their area within the boundary of the figure). Each of these squares is counted as one full square to approximate their area contribution.
- Count Half-Contained Squares: For squares where exactly half of the area lies within the boundary, count each of these as ½ a unit.
- Ignore Squares Less than Half Inside: Any squares with less than half their area inside the figure can be disregarded, as they contribute very little to the area.
Final Calculation
To find the approximate area, use this formula:Approximate Area=Number of Full Squares+Squares More than Half+12(Half-Contained Squares)\text{Approximate Area} = \text{Number of Full Squares} + \text{Squares More than Half} + \frac{1}{2} (\text{Half-Contained Squares})Approximate Area=Number of Full Squares+Squares More than Half+21(Half-Contained Squares)
Example Calculation
Let’s go through an example. Suppose you have a figure placed on grid paper and observe the following:
- Full squares completely within: 6
- Squares more than half inside: 6
- Half-contained squares: 1
Using the formula above:Approximate Area=6+6+12(1)=6+6+0.5=12.5 square units\text{Approximate Area} = 6 + 6 + \frac{1}{2}(1) = 6 + 6 + 0.5 = 12.5 \text{ square units}Approximate Area=6+6+21(1)=6+6+0.5=12.5 square units
Why This Method Works
This approach gives a close approximation of the area of an irregular shape by breaking it down into manageable sections (squares). Although it’s an estimate, it’s effective for real-world applications where precise area measurements are difficult to obtain.
By following these steps, you can confidently estimate the area of any irregular shape. This method is particularly useful for irregularly shaped land plots, custom-designed garden beds, and various DIY projects where accurate area measurement is essential.